On May 7, 2016, Pearlie Mae Smith, the winner of the New Jersey Lottery Powerball, had an enviable decision to make: Should she accept $429 million in payments over 30 years or accept a smaller amount, $284 million, up front? Though it was 34% lower, Ms. Smith chose the up-front payment. While Ms. Smith was more than 70 years old at the time she won the Powerball, her choice was not unique. Powerball data show that all five winners in 2016 chose the up-front payment versus taking payments over time, forfeiting more than a third of their nominal earnings.
Going back as far as 2003, you will find cases where Powerball winners were willing to sacrifice half their winnings to claim them up front versus spreading them out over time. If sacrificing almost half of one’s nominal winnings in exchange for an up-front payment does not sound totally crazy, you already have an intuitive understanding of the concept of the time value of money, also known as discounting.
Time Value of Money
The time value of money means that a dollar promised at a future date is worth a discounted amount compared to a dollar guaranteed today. This is because there is no guarantee that whoever promised you the dollar will be around or will deliver it in 25 years. Even if the person does deliver the dollar, due to inflation, it will not buy as much in 25 years as it does today. In addition, if you get a dollar today, you can invest it and grow that dollar over time. For all of these reasons, money promised in the future is worth less than money guaranteed today.
Discount rate. In the context of solar, the value of electric bill savings in the future should be similarly discounted relative to cash in hand today. The amount that a dollar in the future is discounted relative to a dollar today is referred to as the discount rate, which the American Heritage Dictionary defines as “the interest rate used in determining the present value of a future payment or series of payments.” In plain English, this is the rate of return at which it makes no difference to you whether you receive the payment today versus sometime in the future.
For the mathematically inclined, you can calculate the discount of future to current savings using the following formula:
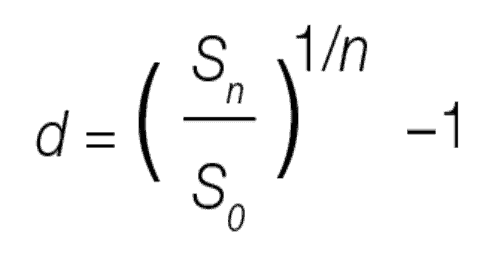 where d is the discount rate, Sn is the savings in year n, S0 is the current value of these savings and n is the year of evaluation. The discount rate is typically expressed as a percentage.
where d is the discount rate, Sn is the savings in year n, S0 is the current value of these savings and n is the year of evaluation. The discount rate is typically expressed as a percentage.
Modeling Financial Returns
If you are not applying a discount rate, or if the software you are using does not do so, you are likely misrepresenting the financial returns of going solar. You may also be making suboptimal solar design decisions or recommending the wrong financing option to your client. Let us examine what the application of a discount rate does to some of the more commonly quoted solar financial metrics—lifetime savings, internal rate of return (IRR), levelized cost of energy (LCOE), and payback period—across two financing options: cash and loan-financed purchase.
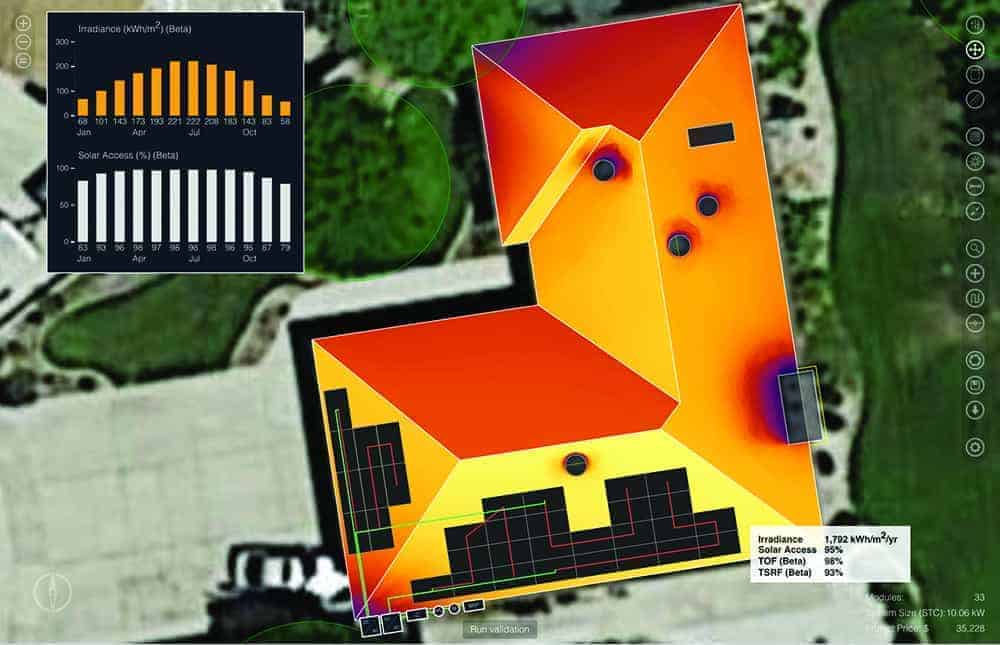
Figure 1. Aurora estimates that the 10 kW array shown here has a weighted total solar resource fraction of 86% and will generate 12.85 MWh of energy in year 1.
Case study. For this example, I used Aurora both to design the 10 kW system in Figure 1 and to perform the financial analysis. The case study assumes the following: The customer is on PG&E’s E-1 baseline utility rate for Region S; the assumed utility inflation rate is 3%; the system cost is $3.50 per watt; the loan terms require 20% down and 4.9% interest; incentives are limited to the 30% Investment Tax Credit; and the project service life is 25 years. The financial results presented in Table 1 (below) show that applying a discount rate leads to a reduction in the present value of lifetime savings and the LCOE, as well as a slightly longer payback period. These results have implications for both the recommended financing option and the optimal system design.
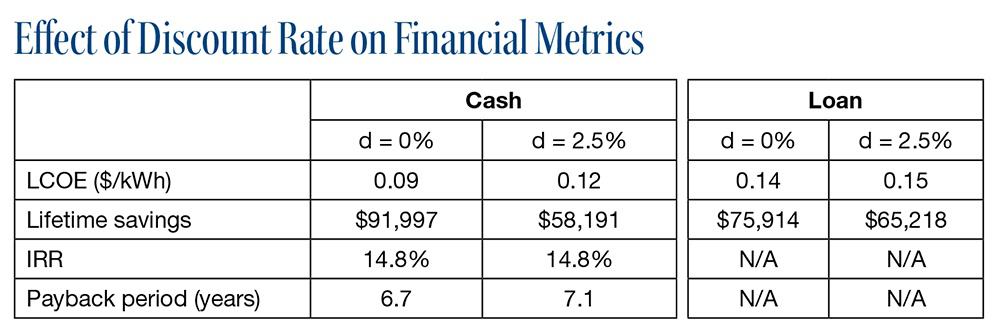 Table 1. A comparison of common financial metrics for a cash purchase versus a 2-year loan-financed system (20% down, 4.9% interest), with and without discounting.
Table 1. A comparison of common financial metrics for a cash purchase versus a 2-year loan-financed system (20% down, 4.9% interest), with and without discounting.
Customer financing: With a 2.5% discount rate, this client’s discounted lifetime savings are greater with a loan-financed system compared to a cash deal. The discount rate acts as a penalty for tying up the cash that the client might have invested in another asset. It is also interesting to observe the changes in LCOE. With a discount rate applied, the LCOE for a cash purchase increases by more than 30%, whereas the LCOE for the loan structure increases by only about 7%. We have already established that a dollar guaranteed today is not the same as one promised in 25 years, and it is equally true that a dollar owed 25 years from now is worth a lot less than one in hand today. Thus, a loan-financed system generally starts to look more favorable relative to a cash purchase as discount rates increase.
Design optimization: Designers can also use LCOE to determine whether a proposed solar installation generates a financially optimal amount of energy. If, on one hand, the effective utility rate is higher than the project’s LCOE, then the homeowner is leaving money on the table by not generating more solar energy. In this case, you should seek to design a higher-producing system to capitalize on the higher utility compensation rate. On the other hand, if the effective utility rate is lower than the LCOE, then the homeowner is losing money on each incremental unit of energy generated. In this scenario, the appropriate design response is to generate less energy, perhaps by specifying less-costly components with lower energy yields.
Analyzing results. While nobody wants to show lower financial returns, the discounted values in Table 1 more accurately reflect the financial returns of going solar. Furthermore, by performing this type of analysis, you can now credibly compare the returns on solar to other asset classes. Even with the 2.5% discount rate, the homeowner is saving more than $58,000 over the project’s life in today’s dollars and is earning an annualized return of 14.8%.
To put a 14.8% return for solar in PG&E service territory in context, State Street Global Advisers forecasts that the US bond and stock markets will have long-term annualized returns of 2.5% and 7.7%, respectively. However, financial markets are volatile, whereas solar provides savings as long as the sun shines (and assuming that regulators do not retroactively change policies). Furthermore, unlike income from the stock or bond markets, solar savings are tax-free. This means that if you provide an apples-to-apples comparison of financial returns, going solar is a no-brainer investment for this particular homeowner, as illustrated in Table 2.
 Table 2. Applying a discount rate allows for an apples-to-apples comparison of potential investment opportunities.
Table 2. Applying a discount rate allows for an apples-to-apples comparison of potential investment opportunities.
Accuracy and credibility. Applying a discount rate when assessing investment decisions is a well-established practice for financial and economic analyses. Many analogous industries have adopted this as standard practice. For example, realtor.com offers an online Rent vs. Buy Calculator where the discount rate—identified as the investment rate of return—is a required input. The U.S. government’s Office of Management and Budget uses discount rates when calculating the financial returns associated with investing in clean energy or energy efficiency projects, as well as for general budgeting purposes. Within the solar industry, the National Renewable Energy Laboratory (NREL) System Advisor Model (SAM) includes a discount rate when calculating financial metrics. In fact, NREL’s user guide for SAM states that the “discount rate acts as a measure of time value and is central to the calculation of present value.”
It is well established that the cost of acquiring customers is one of the major obstacles to making solar ubiquitous. Consumer education is one of the reasons commonly cited for the high cost: Consumers are often confused about the economic benefits of going solar. Perhaps one way to help alleviate this is to speak to homeowners in familiar terms. While most homeowners are unfamiliar with terms like azimuth or solar access, they likely have had to assess how much money to put into a 401k or whether to buy or rent. Moreover, they almost certainly understand that a dollar will not be worth the same in 25 years as a dollar is worth today.
Applying a discount rate as part of your financial analyses not only will improve your design and financial decision-making processes, but will also increase the accuracy and credibility of your results and allow you to make an apples-to-apples comparison between the returns of solar versus other asset classes.